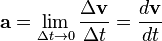En la actualidad, y desde hace siglo, las matemáticas han sido algo esencial para la vida, y así mismo el desarrollo del ser humano, y de la sociedad en conjunto.
Las matemáticas se van jerarquizando, dependiendo su grado de dificultad, por lo que se dividen en ramas, como lo son, la geometría, el álgebra la trigonometría, la estadística, las matemáticas en general, y algo muy peculiar llamado calculo, tanto integral como diferencial.

Al escuchar esta última rama de las matemáticas, se piensa que es algo muy complejo, lo cual no tiene ninguna aplicación en la vida diaria, pero al profundizar más en el tema, se encontrara que es todo lo contrario.
El cálculo diferencial, se puede aplicar en la economía, la administración, la física, etc. Los principales elementos que se utilizan el esta rama de las matemáticas, son las funciones, las derivadas, los sistemas de ecuaciones, la pendiente, entre otros; que estos a su vez en conjunto ayudan a realizar grandes calculo en importantes empresas, o simples operaciones en la economía familiar.
Las principales aplicaciones del cálculo diferencial son:
• El estudio de movimientos, aspectos de velocidad, y aceleración.
• El cálculo de máximos y mínimos, por ejemplo:
- En una agencia de viajes, o en una empresa, saber cuál es la mayor ganancia que se puede obtener en cierto periodo, o con cierto producto, pero a la vez, igualmente calcular, si existen perdidas en estos productos, o en un lapso de tiempo. Si se aplica de manera correcta el cálculo diferencial, se podrán obtener estos resultados, sin ningún problema.

En economía los costos marginales, los ingresos marginales y las utilidades marginales también son derivadas. Una aplicación interesante de la derivada se encuentra en los problemas de optimización. Por ejemplo, cuando una compañía que elabora bebidas desea reducir costos produciendo una lata que contenga el máximo volumen y requiera el mínimo de material, la solución puede encontrarse mediante el empleo del cálculo diferencial.
El cálculo tiene amplias aplicaciones en la ciencia y la ingeniería y se usa para resolver problemas para los cuales el álgebra por sí sola es insuficiente.
.